The following unedited text has been submitted to Knitting Industry by Sunil Kumar Puri, Executive Director of Sportking Institute of Fashion Technology, Ludhiana, India. Sunil has over 30 years experience in the knitting industry, is a qualified professional in Total Quality Management, Kaizen and Lean Production and runs his own knitting machinery sales company, Techknit Overseas Pvt. Ltd.

The paper attempts to explain ‘Sweater Geometry’ for fully-fashioned knitwear, to explain the size chart and give in depth knowledge to the reader about the hidden measurements which are needed to make a good sweater.

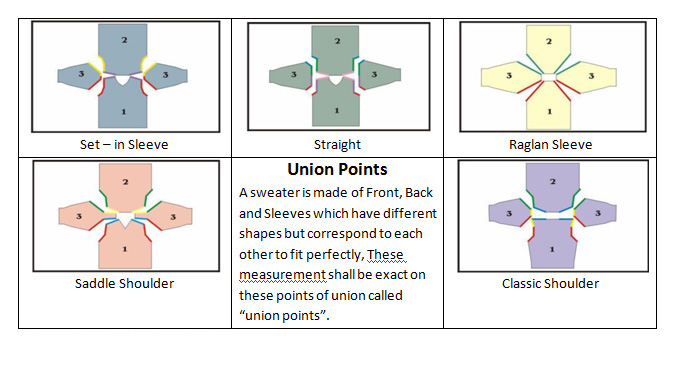
“The fully Fashioned Sweaters can be classified in five different shapes, Set-in Sleeve, Straight, Raglan, Saddle Shoulder and Classic. Examples of these styles are given in pictures given below.  The beauty of the garment lies in the accurate fitting of the union points of front back and sleeve. The common mistake is that most of the times, as these panels knitted and not woven, the loops compensate for the deficiencies of the shapes of front, back and sleeves. The garment may measure accurately but the expert eye will always know that because of the inaccuracy of panels, the stitches or knit loops do get distorted and are not aligned any more. A very nicely made garment when placed on a table shall have all the courses and wales in straight lines, which at times becomes very difficult to achieve and the arms of the sweater shall extend at the same angle as that of the shoulder slope. The sleeves shall not puff out at the shoulder joint nor shall they cave in. Therefore the most important measurement in a sweater is the slope of the arm hole as the angle so created shall be the angle of the sleeve joint as well. Surprisingly the shoulder slope is not given the due respect by the knitters that it demands.

The calculations of knitting specifications are based on combination of simple mathematics and the Pythagoras theorem of Geometry. In most of the cases the dimensions given by the customer are as given under in two different sets, the first one where the sleeve length is given as under sleeve length this practice is more common in UK and the other in which the sleeve length is given for the upper part of the sleeve. 

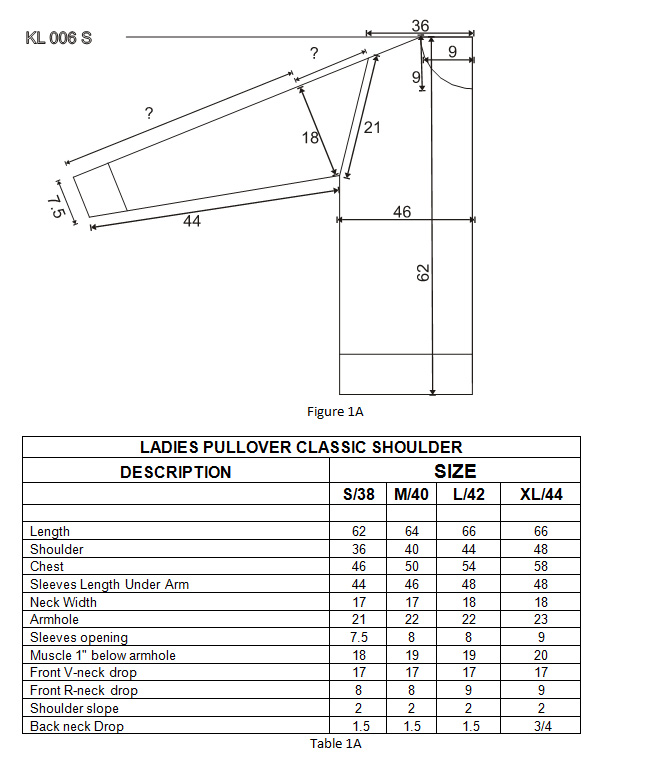
But in both the cases the measurement of the actual length of the sleeve up to the part where it has to join the body is not given. Also the side length of the body where the sleeve has to join the body is rarely provided by the buyer.  By simple calculations and by applying the Pythagoras theorem we can make all the calculations precisely and accurately. If we look at the picture 1A which represents the table 1A we can draw that whereas the measurement for the under sleeve is provided it does not tell us what length has to be knitted to achieve the under arm length.  Similarly it does not tell us how much of the sleeve head ( crown or cap) has to be knitted so that it does not just fits in the joint of the front and back properly but also maintains the angle of slope of the shoulder. Slight variation will lead to the change in the angle of the sleeve with the horizontal plane that starts from the back neck of the garment. If at this point the sleeve cap is larger than required it will make the angle steeper than that of the shoulder and may also result in a protruding bulge at the joint of shoulder. The opposite of this will give opposite results i.e., the angle will become shorter than that of the shoulder slope giving wing like shape to the sleeve and the sleeve joint may also show a caved-in effect at the joint.

Before we go further we must understand the basic principles of the Pythagoras theorem as well as elementary trigonometry.

The values of Sin Ç¿ and Cos Ç¿ can be easily obtained by using a scientific calculator or trigonometric tables. What we learn from this is that if we know any two values the third can be calculated using simple calculations i.e., if we know the hypotenuse and the adjacent we can find the value of the opposite, and if we know the hypotenuse and the opposite we can calculate the adjacent and if we know the values of the adjacent and the opposite we can calculate the hypotenuse. Also by using simple trigonometric functions if we know the value of either of the hypotenuse, the adjacent or the opposite and any of the angle other than the right angle we can find the value of all other arms of the triangle or if we know the value of any two sides of the triangle we can not only find the value of the third one but also the angle of the triangle.

Angle of Shoulder Slope

As discussed earlier to knit a good sweater “the arms of the sweater shall be at the same angle as that of the shoulder slope”. It therefore becomes necessary to ascertain the angle of the Shoulder Slope.  Normally the buyer provides shoulder drop as a measurement for all sizes. At times this measurement is same as mentioned by the customer. If we keep the drop as same for all sizes the angle of shoulder drop will vary for all the sizes.

In cut and sew garments there is no problem but the three basic fully fashioned garments i.e., Raglan, Saddle Shoulder and Classic style the shoulder slope angle has to be maintained and therefore it is necessary to understand how to obtain the shoulder slope angle and the angle that regulates the measurement of the sleeve cap or crown and its width.

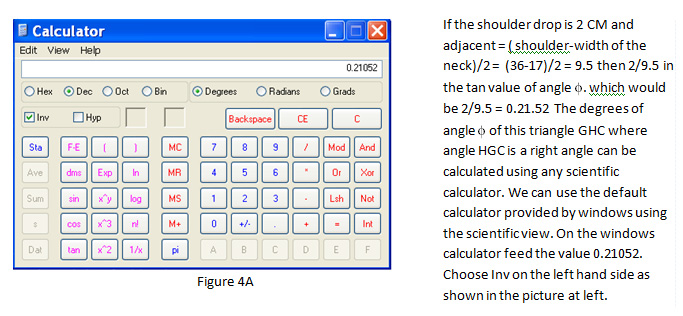
The triangle GCH represents the angle of the shoulder slope. If we know the value of the Shoulder drop i.e., GC we can easily deduce the value of the adjacent i.e., GH. GH = (Shoulder width-Neck Width)/2. We also know the value of the opposite i.e., GC. The angle between GHC can be easily calculated using simple trigonometric formulas.  The simple way to find the Angle would be Opposite /Adjacent = Tanf.

Angle of the Arm Hole

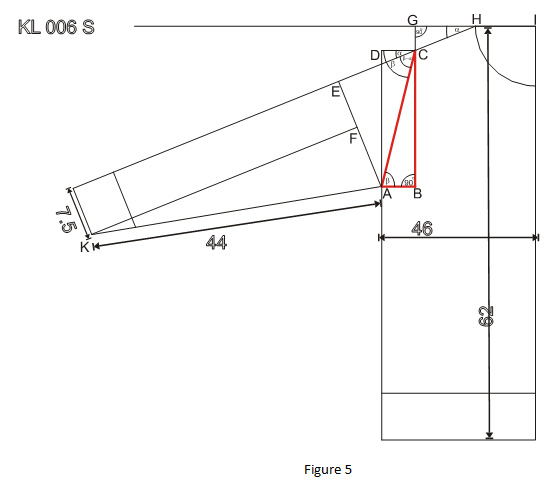
The arm hole of a sweater is measured from point to point i.e., from the point where under sleeve and the over sleeve join the main body, i.e., A and C in the figure 5. The Arm AC hole is the hypotenuse of the triangle ABC formed by the Arm Hole, where AB is the adjacent and the BC is the opposite. It is not important to know the valve of the angle CAB alone. It is also important to know the value of the opposite the distance between B and C. Knowing this value we will know where on the side body the sleeve has to be attached. By knowing this value we can measure the side length of the garment. This point will be = (Total length of the garment – the shoulder drop – the opposite of the Arm Hole) and needless to mention that seam margin has to be added to it, as it has to be added for all other seam margins. So as per the figure 5applying the Pythagoras theorem a² + b² = c², BC=√ (AC²- AB²)

And the angle of the Arm Hole with the base of the garment or the back of the neck of the garment can be calculated using the scientific calculator as described before. The angle of the Arm hole and the opposite in the case will be:

BC = √ (21² - 5²) = √416 = 20.39 or let us say 20.4

The angle CAB will be sin⁻¹ 20.4/21 i.e., inverse of the sine of Opposite/Hypotenuse = 76.27 or say 76°

The side length of the Garment = 60 – 2 – 20.4 = 37.6

Defining the Angle of the Arm

Once the Angle of the Arm hole is obtained it is important to know the angle of the Arm or the angle of ACE. This angle will provide us calculations for the crown as well as the sleeve width at the point of the joint with the main body of the garment.  For this we need to ascertain the value of the angle ACE.

 The figure above shows the triangle ACE as well as triangle ABC to understand the value of the angle between ACE we need to study the Rectangle ABCD so we enlarge the area of the rectangle ABCD in figure 6B

Let us presume the angle CAB is β and ABCD being a rectangle the angle DCA will also be angle β. This is also the angle of the arm Hole which we have calculated as 76° in our earlier calculation.  The angle between DCE is also equal to the Angle between GHC (angle of Shoulder Slope and calculated as 12 in our earlier calculation. The Angle ACE = Angle ACD β - Angle DCE α = 76°-12°=64°

Calculations of the Sleeve Width and the Sleeve Cap

Once we know the value of the angle between ACE we can also not just obtain the value of the crown and the width of the sleeve, we can also cross check the width of the sleeve as provided by the customer.  At times the sleeve width provided by the customer is little over or under the exact value which often falls in the tolerance range set by the customer or the industry standards. The other reason why the sweater still will be sew-able is that the knitted panels adjust to such irregularities to quite an extent because of the nature of the loop structure which can rob and get robbed by the next loops. The idea here is to set a target which is accurate, if we have an accurate target and if our aim is accurate our result will be too close to the target considering there can be some special causes which may deter us from getting the desired results. But if our target is hazy, our aim is not right the special causes may play havoc with our results. And we may not be able to drive at the root cause of the problem.  If our calculations are right and if still don’t get the desired results it certainly mean presence of special causes, but if our calculations are challengeable the results may point towards presence of special causes which may not be there and unnecessary time effort and money may be spent on trying to apprehend a nonexistent ghost.

If we refer to figure 7, if we know the angle between ECA and if we know the value of AC i.e., the Arm Hole, we can reconfirm the width of the sleeve as well as we can ascertain the value of CE the crown or Cap of the sleeve.

For the width the equation to be used can be any of the three equations described in figure 2. But we will use the equation Opposite / Hypotenuse = Sin f ,  AE/AC= Sinf or AE= AC* Sin f. Here the width of the sleeve according to mathematical and trigonometric calculations will be. 

The sin of angle 64° = 0.8987940

The product of sine of 64° and Arm Hole = 18.874 or let us say 18.9 CM.

The width according to the measurements supplied by the customer say 18 which may be a bit too short and shall be replaced by let us say 19 cm. The variation may be within the tolerance and thus a supplier may get his garment approved barely even if his measurement is more accurate. A garment with exact muscle measurement may not look good at all. Therefore understanding of these calculations can save a lot of tense moments during the inspections conducted by the customer and especially by the third party. The customer may see your point of view but the third party inspector has to stick to the rules and may reject the shipment which was a perfect shipment.

Similarly the crown of the sleeve which is also responsible for maintaining the angle of the shoulder slope throughout the length of the sleeve can also be calculated as:

Adjacent / Hypotenuse = Cos f

EC / AC = Cos f  or EC = AC * Cos 64° or EC= 21 *0.4383 = 9.2

The Exact Length of the sleeve where it joins the main body at lower Arm Hole point.

By calculating the Opposite of the Arm Hole we were able to ascertain the length where the sleeve shall join the lower point of the Arm Hole, but the exact sleeve length where it shall join the main body has to be ascertained and the total sleeve length is not the answer. The Total Sleeve length – The crown of the sleeve which also matches with the width of the sleeve shall be the measurement of the sleeve length where the sleeve shall join with the Main Body. But if the customer has provided us the under sleeve length as a standard measurement, the following calculation has to be made. Please refer to Figure 8 given below. If we know the value of underarm Length, and we know the value of maximum width of the sleeve as calculated earlier, and the cuff width which is 7.5 then we know the value of AF as AE – cuff width = 18.87- 7.5 = 11.37. The value of the line between K and F can be calculated using Pythagoras theorem as SQRT of (44*44-11.37*11.37) = 42.5. This means we have to knit 42.5 Cm of sleeve length to knit to the joining point of the sleeve with the body and the increment of the sleeve width will compensate of the balance 1.5 Cm, of course some margin for the seat of the sleeve as well as seam margin has o be kept in mind.

Conclusions

Using these simple calculations which shall not take more than five minutes and if an excel sheet is prepared for different styles using the necessary formulas the correct measurements required to knit a perfect garment becomes a child’s play.  An understanding of these calculations also helps the knitter to point out the corrections needed if any in the measurement sheets supplied by the customer. These calculations not only will save a lot of time effort and money but will also give more confidence to the knitter.”